みなさんこんにちは!おさかなです!
今回から「誰でもわかる基本情報シリーズ」というテーマで「基本情報技術者試験」に合格するための知識をご紹介していきます!
第12弾は「論理演算と論理回路」について、書いていこうと思います!
それでは、レッツゴー!!!!!
・「基本情報技術者試験」を受験しようと思っている人
・「基本情報」に必要な知識を身に着けたい人
・IT初心者の人
前回の復習
前回は「シフト演算」の分類や方法について見ていきました。

今回は「論理演算と論理回路」について学習していきたいと思います!
論理演算とは?
コンピューターはさまざまな計算や処理を行いますが、それらは今まで学習してきた「算術演算」(足し算や引き算など)か「論理演算」によって実行されます。
「論理演算」とは、「ある事柄が〇か×か」を判断する演算のことです。
ここでもコンピューターは0と1しか理解できないので、「〇のときは1」、「×のときは0」という風に表現します。
論理回路と表記方法
コンピューターには論理演算を行うための「論理回路」が組み込まれています。
論理回路とは、入力された値に対して論理演算を行い、結果を出力する装置です。
論理回路は、ひと目でわかりやすいように「MIL記号(ミル記号)」と呼ばれる記号を使って図にします。
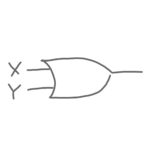

なるほど!パッと見てわかるから「MIL(見る)記号」なんだね!

うんうん。って…!ダジャレかよ!!!!
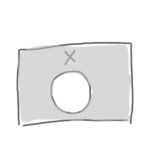
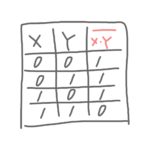
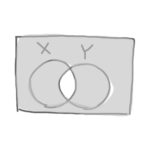
ほかにも条件と答えを一覧にした「真理値表」や、当てはまる部分に色を塗って図で表す「ベン図」も使われます。
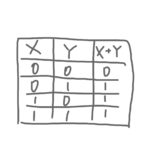
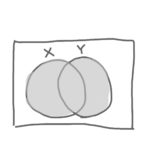

あ!この「ベン図」ってやつ、ナビまるが2人もくっついてるよ!

うんうん。僕が…って!
誰がベン図だあ!

ごめんごめん…💦
基本回路
もっとも基本的な回路である、論理和(OR)、論理積(AND)、否定(NOT)の3つについて順に解説していきます!

プログラミングでも「論理演算子」として、よく使用する3つだね!
論理和(OR)
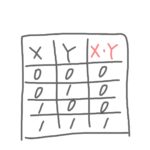
「論理和」は、XかYのどちらか一方でも1ならば、答えが1になる論理演算です。
逆に言うと、どちらも0の場合だけ、答えが0になります。
「+」



論理積(AND)
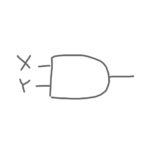
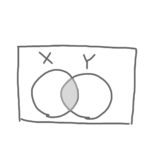
「論理積」はXとYがどちらも1の場合に、答えが1になる論理演算です。
どちらかが0だったり、どちらも0だったりすると、答えは0になります。
「・」
否定(NOT)
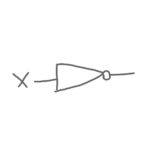
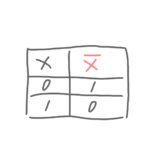
「否定」はXが0であれば、答えは1になり、逆にXが1であれば、答えが0になる論理演算です。
「-」
基本回路の組み合わせ
基本回路は「論理和」「論理積」「否定」の3つですが、これらをうまく掛け合わせたものがいくつかあるのでご紹介していきます。
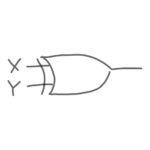
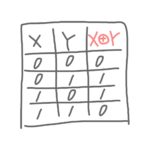
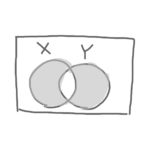
排他的論理和(XOR)
「排他的論理和」とは、XとYが異なる場合に答えが1になり、同じ場合には0になる論理演算です。
「⊕」
否定論理和(NOR)
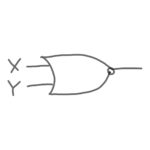
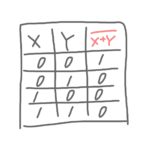
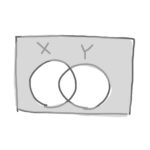
「否定論理和」とは、XとYのどちらか一方でも1の場合に答えが0になる論理演算です。
「論理和」+「否定」
記号
「+」と「-」
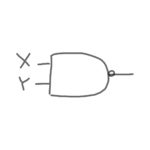
否定論理積(NAND)
「否定論理積」とは、XとYがどちらも1の場合に答えが0になる論理演算です。
「論理積」+「否定」
記号
「・」と「-」
ド・モルガンの法則
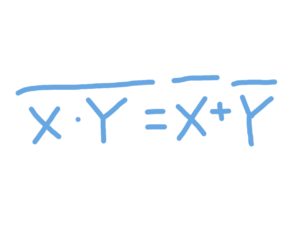
…論理積全体の否定派、それぞれの否定の論理和
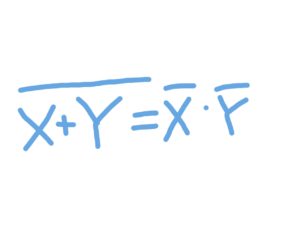
…論理和全体の否定派、それぞれの否定の論理積

高校の数学で勉強したところだ!
今回の学習内容まとめ
・「論理演算」とは、「ある事柄が〇か×か」を判断する演算のこと。
「〇のときは1」、「×のときは0」
・「論理回路」とは入力された値に対して論理演算を行い、結果を出力する装置のこと。
・論理回路を表現する方法として、「MIL記号(ミル記号)」「真理値表」「ベン図」がある。
・基本回路3つ、論理和(OR)、論理積(AND)、否定(NOT)
・組み合わせ回路、排他的論理和(XOR)、否定論理和(NOR)、否定論理積(NAND)
・ド・モルガンの法則

しっかり復習しておこう!
おさかなが参考にした「書籍」一覧↓
・(PDF・スマホ単語帳付)かんたん合格 基本情報技術者教科書 令和2年度
・令和02年 イメージ&クレバー方式でよくわかる 栢木先生の基本情報技術者教室 情報処理技術者試験
・キタミ式イラストIT塾 基本情報技術者 令和02年 (情報処理技術者試験)
感想・まとめ
今回は「論理演算と論理回路」について、書いていきました…!
いかがだったでしょうか?
論理演算と論理回路は、図や表を用いた試験問題が多く出題されるので、記号と意味を確実に押さえておくと良いでしょう。
↓次回は「半加算器と全加算器」について解説していきます!

お楽しみに~!
おさかなびではプログラミング学習中の人、ブログ初心者に向けて、「デジタル時代を楽しむためのミニ知識」をご紹介しています!
ぜひ他のページも覗いてみてください…!
それでは今回はこの辺で!
ここまで読んでくださり、ありがとうございました!
おさかなでした!
【おさかなび-osakanav-】では、この記事の感想!おさかなへの応援メッセージ!おさかなに聞きたい事、質問!記事にしてほしい内容!などを大募集中!
「氏名」「メールアドレス」「内容」の3点をご記入の上「osakana1699@gmail.com」までご応募ください!


